次回作について

どうも!次回作として敵と鬼ごっこをするような
ゲームを考えています!
つまりどこまでもプレイヤーを追いかけてくるような敵ですね。
ということで今回は敵の移動処理について考えてみようと思います!
敵の移動アルゴリズムを考えるのって結構レベル高いっすよね…
あんまり考えたくないというか頭がコングラッチュレーションになるというか
日本の未来はWow Wow Wow Wowっていうか…
でもまぁついにやってみようと決意したのでやったことを
以下に記載していきます。
(どちらかというと最短経路の計算がメインです)
ではいきましょー
Unity 3Dの場合はnavMeshで解決!

ムズイのでまず最初にUnityの標準機能で
勝手にやってくれるのないかなって探したのですが
残念ながら2Dの場合はありませんでした。
3Dの場合はnavMeshという機能を使えば結構簡単に
経路探索するように出来るようなのですが
2Dに対応していないみたいなんですね…。
あとアセットとしては以下が人気あるようです
リンク先で動画が見れますが有料なだけあって
結構すごいです
ということで2Dではどうしたらいいのか?を
調べたら結果として自分で作るしかないということが分かりました。
(違ってたらごめんなさい)
A*アルゴリズム

ということで2Dでやるならスクリプト自作で乗り切るしかないのですが
じゃぁどうやって実装すればいいのか?っていうと
A*(エースター)アルゴリズムが妥当だろうと思いました。
このアルゴリズムを簡単に説明すると
経路を検索するアルゴリズムです。
正直A*の内容についてはwikipediaが分かりやすく説明してくれているので
そちらを参考にしていただければと思います。(本末転倒!!)
正直今回は自分の説明が分かりにくすぎるので完全自分用記事です。苦笑
A*の概要

A*で経路探索する手順をザっと以下に記載します。
とりあえず分けると以下3手順です。
1.マップを作る (移動できる範囲を決める)
2.スタート地点とゴール地点を設定
3.どうすれば最短でスタートからゴールまで行けるか考える!
正直1と2はA*以前の問題で3がA*の本題です。
それぞれ解説していきます。
マップを作る
そもそもの地形を設定します。
これがないと始まらないですね。
一番わかりやすいのは碁盤の目状の地図だと思います。
なのでここでは私が好きなtilemapで移動できる地図を作成します。
とりあえず以下のようなものを作りました!
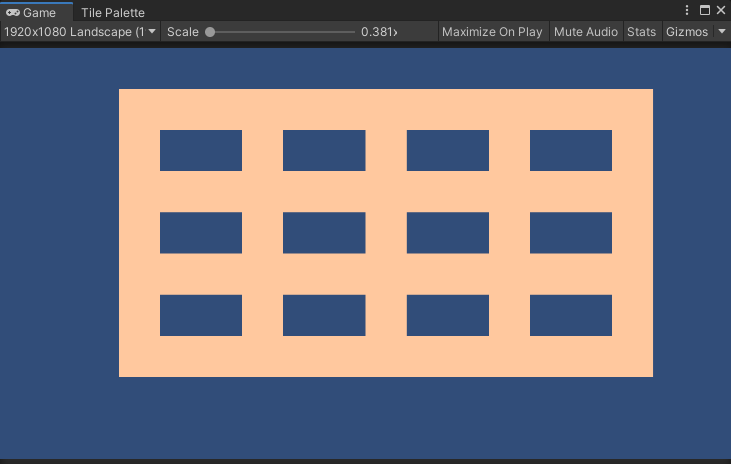
これは単純に長方形型のタイルを碁盤目状にパパっと生成しただけです。
そもそもTilemapってなに?って方は以前isometric型のTilemapの作り方を説明した記事があるので
そちらを参考にしてみてください。
今回はrectangle型で作っているのでisometricよりも簡単だと思います。
スタート地点とゴール地点を設定
スタート地点とゴール地点を設定します。
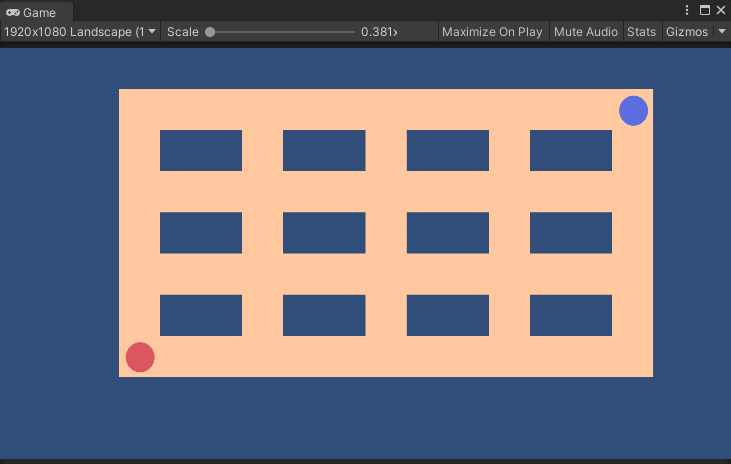
ここではそれぞれ以下にしました。
スタート地点:敵の位置(上記画像の赤い丸)
ゴール地点:プレイヤーの位置(上記画像の青い丸)
どちらもゲームオブジェクトとして生成しています。
どうすれば最短でスタートからゴールまで行けるか考える!
スタート、ゴールが設定できたら
本題のどうすれば最短でスタートからゴールまで
行けるか?ですよね。
正直以下では私自身が理解しやすいように
かみ砕いて説明しています。
たまに説明が間違っているかもしれませんがご容赦ください…
結構説明長いので
あんまり興味ないよってかたは実装のところまでスキップしてね!
そもそもA*はゴール地点の位置が分かっている状態で
実行できるアルゴリズムです。
ゴールが分かってないと実行できません。
A*では
今まで歩いた歩数
と
今の地点からゴールまでの距離
の二つの要素で判定します。
最終的にゴールまで歩いた歩数が最小であれば最短になりますよね。
で、「今の地点からゴールまでの距離」は
これがあると早く処理が終わりやすいんです。
逆にゴールまでの距離を求めないと処理が遅くなりがちです。
なぜかというと経路探索って基本、総当たり的に検索するからです。
現実世界ではどっちに行けばいいか分からないときに匂いなどの
ヒントとなる情報が存在していますがパソコン上ではそういった情報は
存在していませんね。
例えば現実世界でバーベキューしている場所に行きたいけどどっちに
行けばいいか分からない時に肉を焼いているいい匂いを頼りに
どっちに移動すればいいか、なんとなく分かったりしますが
パソコン上ではそういった情報は自分が作らない限り存在しません。
ということで、どこに歩けばいいか分からないから全ての方向に
歩こうとするわけです。当然ゴールと真逆の方向にも行こうとします。
もしかしたらそれが正解かもしれないのですが
ゴールの位置を知っている状態であれば
なんとなくゴールとの距離が近づいていく方が正しい気がしませんか?
例えば私たちも道に迷ってどっちに行ったらいいか分からないけど
行きたい場所は北の方角にある、で、コンパスを持っている。
っていう状況だったらコンパスの示す北の方向にとりあえず進みますよね。
北の方向にゴールがあるのに南に行こうと考える人ってなかなかいないと思います。
そういった「コンパス」みたいな指針と考えてください。
で
歩いた歩数 = 実コスト
ゴールまでの距離 = 推定コスト
総コスト = 実コスト + 推定コスト
と名付けましょう。
それぞれの地点で総コストを算出して
総コストの小さい地点から経路を検索していくんです。
(ここでいう「それぞれの地点」はTileBase、つまりタイル1個1個のことです)
これでなんにも考えずに経路を探すよりは早く
最短経路が見つかりやすいというわけです。
A*を具体的に考える
では更に具体的に考えていきましょう。
分かりやすくするために以下のような単純な碁盤の目状の
マップにスタート地点とゴール地点があるという状況だとします。
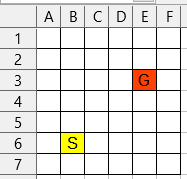
一番最初は当然スタート地点にいます。
1歩づつ歩くとしてスタート地点から歩ける場所は
今回は碁盤の目状なのでスタート地点を中心とした
8マス(青く塗った箇所)になりますね。
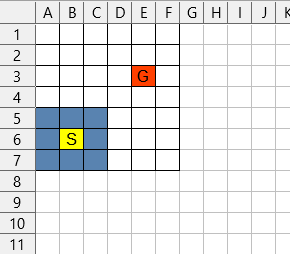
この8マスを検索対象のマスとして記憶しておきます。
で、この8マスにはどこから歩いてきたか?
という情報を記憶しておきます。
これを親マスと呼びましょう
現在、スタート地点から1歩歩いただけなので
親マスはスタート地点になります。
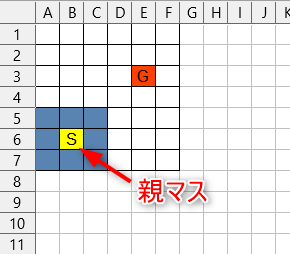
スタート地点はこれで処理が終わったので
終わったよーってことを記憶しておきます。
では次にスタート地点の周りの8マスを順番に検索していきます。
この時全部で8回調べるのですが無作為に調べるよりも
調べる優先順位をつけて処理を速く終わらせたいです。
(大きなマップほど処理時間がかかってしまうので出来るだけ
処理を軽くしたいわけです。)
という技術者的諸事情があるわけですがそうは言っても
どれから調べた方がいいか?っていう判定が難しいですよね。
そこで推定コスト(ゴールまでの距離)の出番です。
もっとちゃんというと総コストの出番なのですが
今のところ一歩しか歩いていないので実コストはどのマスも
同じになり違いは推定コストだけです。
8マスそれぞれのゴールまでの距離を計算するわけです。
するとゴールに近いほうが総コストが低くなりますね。
ゴールと真逆にいくと総コストが高くなります。
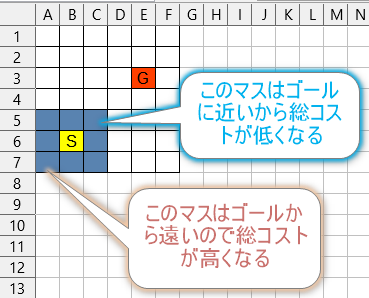
ということで総コストが低いマスから優先的に調べていきます。
例えば今回は右上のマスがゴールに近いので
最優先に調べるのは右上のマスです。
ということで次は右上のマスを中心とした8マスについて考えます。
この中で左、左下、下のマスはスタート時点で調査対象になっているので
特に処理しません。
それ以外のまだ調査対象になっていないマスを調査対象として記憶します。
以下では緑色のマスですね
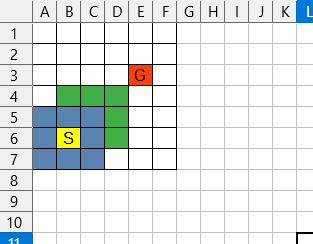
この時初めて検索対象となるマスの
実コストは2歩目になることに注意です。
スタート地点から考えると二歩目ですからね。
三歩目も同じように調べますが既にゴールにたどり着きます。
こんな感じでループしていきます。
コストの一番低いマスを検索する
↓
その周りを検索対象にする(中心のマスは検索終わったよーって記憶する)
↓
総コストを計算し親マスを記憶する
↓
コストの一番低いマスを検索する
…
こんな感じですね。
これをゴールがみつかるまで
ひたすら繰り返します。
万が一全てのマスの検索が終わってしまっても
ゴールに辿り着けなかったらゴールまでいくことは
不可能だったって分かるわけです。
ゴールが見つかった場合は記憶していた
親マスを順番に辿っていきます。
すると最初のスタート地点までの最短経路が分かる
というカラクリです!
A*を実装してみる

では実際に実装してみましょう。
今回はボタンを押したら
スタート地点とゴール地点を結ぶ最短経路の
タイルの色が変わる処理を実装します。
まずは空のスクリプトを生成します。
AStarPathという名前のスクリプトを作成しました。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class AStarPath : MonoBehaviour
{
// Start is called before the first frame update
void Start()
{
}
// Update is called once per frame
void Update()
{
}
}
最初に実コスト、推定コスト、総コスト、親パス、調査対象かどうかとか色々記憶しておくべき
要素があるので、そういったクラスを作成します。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class cellInfo
{
public Vector3 pos { get; set; } // 対象の位置情報
public float cost { get; set; } // 実コスト(今まで何歩歩いたか)
public float heuristic { get; set; } // 推定コスト(ゴールまでの距離)
public float sumConst { get; set; } // 総コスト = 実コスト + 推定コスト
public Vector3 parent { get; set; } // 親セルの位置情報
public bool isOpen { get; set; } // 調査対象となっているかどうか
}
public class AStarPath : MonoBehaviour
{
// Start is called before the first frame update
void Start()
{
}
// Update is called once per frame
void Update()
{
}
}
上記の通りここではcellInfoっていうクラスを作成しました。
続いて本題のA*の処理を以下に記載しました。
色の変わっているところが追加した部分です。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.Tilemaps;
using System.Linq;
public class cellInfo
{
public Vector3 pos { get; set; } // 対象の位置情報
public float cost { get; set; } // 実コスト(今まで何歩歩いたか)
public float heuristic { get; set; } // 推定コスト(ゴールまでの距離)
public float sumConst { get; set; } // 総コスト = 実コスト + 推定コスト
public Vector3 parent { get; set; } // 親セルの位置情報
public bool isOpen { get; set; } // 調査対象となっているかどうか
}
public class AStarPath : MonoBehaviour
{
public Tilemap map; // 移動範囲
public TileBase replaceTile; // 移動線上に位置するタイルの色を代える
public GameObject player; // プレイヤーのゲームオブジェクト
public GameObject enemy; // 敵のゲームオブジェクト
private List<cellInfo> cellInfoList; // 調査セルを記憶しておくリスト
private Vector3 goal; // ゴールの位置情報
private bool exitFlg; // 処理が終了したかどうか
// Start is called before the first frame update
void Start()
{
cellInfoList = new List<cellInfo>();
astarSearchPathFinding();
}
// Update is called once per frame
void Update()
{
}
/// <summary>
/// AStarアルゴリズムです。
/// </summary>
public void astarSearchPathFinding()
{
// ゴールはプレイヤーの位置情報
goal = player.transform.position;
// スタートの情報を設定する(スタートは敵)
cellInfo start = new cellInfo();
start.pos = enemy.transform.position;
start.cost = 0;
start.heuristic = Vector2.Distance(enemy.transform.position, goal);
start.sumConst = start.cost + start.heuristic;
start.parent = new Vector3(-9999, -9999, 0); // スタート時の親の位置はありえない値にしておきます
start.isOpen = true;
cellInfoList.Add(start);
exitFlg = false;
// オープンが存在する限りループ
while (cellInfoList.Where(x => x.isOpen == true).Select(x => x).Count() > 0 && exitFlg == false)
{
// 最小コストのノードを探す
cellInfo minCell = cellInfoList.Where(x => x.isOpen == true).OrderBy(x => x.sumConst).Select(x => x).First();
openSurround(minCell);
// 中心のノードを閉じる
minCell.isOpen = false;
}
}
}
検索対象のセルはリストに入れてLinqでデータ取得を行っています。
ゲームスタートと同時にA*処理が実行されるようにしました。
周りのセルを調査する処理(openSurround())を追加したのが以下です。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.Tilemaps;
using System.Linq;
public class cellInfo
{
public Vector3 pos { get; set; } // 対象の位置情報
public float cost { get; set; } // 実コスト(今まで何歩歩いたか)
public float heuristic { get; set; } // 推定コスト(ゴールまでの距離)
public float sumConst { get; set; } // 総コスト = 実コスト + 推定コスト
public Vector3 parent { get; set; } // 親セルの位置情報
public bool isOpen { get; set; } // 調査対象となっているかどうか
}
public class AStarPath : MonoBehaviour
{
public Tilemap map; // 移動範囲
public TileBase replaceTile; // 移動線上に位置するタイルの色を代える
public GameObject player; // プレイヤーのゲームオブジェクト
public GameObject enemy; // 敵のゲームオブジェクト
private List<cellInfo> cellInfoList; // 調査セルを記憶しておくリスト
private Stack<cellInfo> pathInfo; // 最短経路情報のみを記憶しておくスタック
private Vector3 goal; // ゴールの位置情報
private bool exitFlg; // 処理が終了したかどうか
// Start is called before the first frame update
void Start()
{
cellInfoList = new List<cellInfo>();
astarSearchPathFinding();
}
// Update is called once per frame
void Update()
{
}
/// <summary>
/// AStarアルゴリズムです。
/// </summary>
public void astarSearchPathFinding()
{
// ゴールはプレイヤーの位置情報
goal = player.transform.position;
// スタートの情報を設定する(スタートは敵)
cellInfo start = new cellInfo();
start.pos = enemy.transform.position;
start.cost = 0;
start.heuristic = Vector2.Distance(enemy.transform.position, goal);
start.sumConst = start.cost + start.heuristic;
start.parent = new Vector3(-9999, -9999, 0); // スタート時の親の位置はありえない値にしておきます
start.isOpen = true;
cellInfoList.Add(start);
exitFlg = false;
// オープンが存在する限りループ
while (cellInfoList.Where(x => x.isOpen == true).Select(x => x).Count() > 0 && exitFlg == false)
{
// 最小コストのノードを探す
cellInfo minCell = cellInfoList.Where(x => x.isOpen == true).OrderBy(x => x.sumConst).Select(x => x).First();
openSurround(minCell);
// 中心のノードを閉じる
minCell.isOpen = false;
}
}
/// <summary>
/// 周辺のセルを開きます
/// </summary>
private void openSurround(cellInfo center)
{
// ポジションをVector3Intへ変換
Vector3Int centerPos = map.WorldToCell(center.pos);
for (int i = -1; i < 2; i++)
{
for (int j = -1; j < 2; j++)
{
// 上下左右のみ可とする、かつ、中心は除外
if (((i != 0 && j == 0) || (i == 0 && j != 0)) && !(i == 0 && j == 0))
{
Vector3Int posInt = new Vector3Int(centerPos.x + i, centerPos.y + j, centerPos.z);
if (map.HasTile(posInt) && !(i == 0 && j == 0))
{
// リストに存在しないか探す
Vector3 pos = map.CellToWorld(posInt);
pos = new Vector3(pos.x + 0.5f, pos.y + 0.5f, pos.z);
if (cellInfoList.Where(x => x.pos == pos).Select(x => x).Count() == 0)
{
// リストに追加
cellInfo cell = new cellInfo();
cell.pos = pos;
cell.cost = center.cost + 1;
cell.heuristic = Vector2.Distance(pos, goal);
cell.sumConst = cell.cost + cell.heuristic;
cell.parent = center.pos;
cell.isOpen = true;
cellInfoList.Add(cell);
// ゴールの位置と一致したら終了
if (map.WorldToCell(goal) == map.WorldToCell(pos))
{
cellInfo preCell = cell;
while (preCell.parent != new Vector3(-9999, -9999, 0))
{
map.SetTile(map.WorldToCell(preCell.pos), replaceTile);
preCell = cellInfoList.Where(x => x.pos == preCell.parent).Select(x => x).First();
}
exitFlg = true;
return;
}
}
}
}
}
}
}
}
なんかもう説明があれなんでコードを読んで感じ取っていただければと思います。。苦笑
これで完了です!
この状態でゲームスタートボタンを押した時のイメージが以下になります。

めっちゃシンプルな動画ですが
グレーの床が生成されているのが分かると思います。
このグレーの床が今回のA*で計算された最短経路になります!
ちゃんと動きましたね!!
おわりに
いかがでしたでしょうか!
頑張ればこういった処理もなんとか実装できました!



